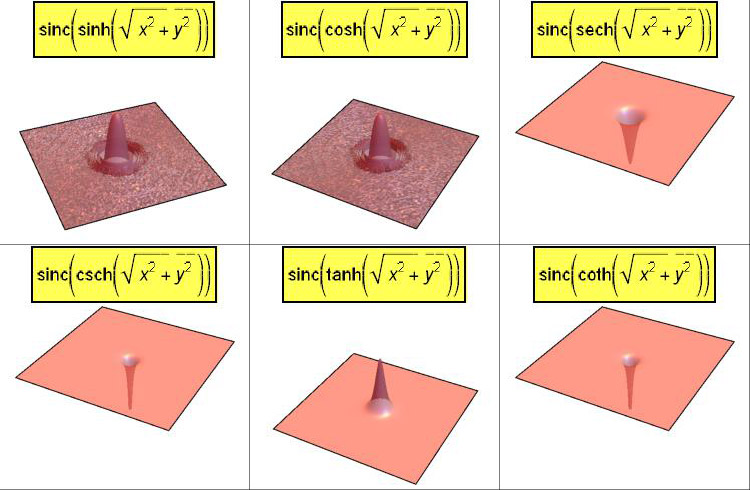
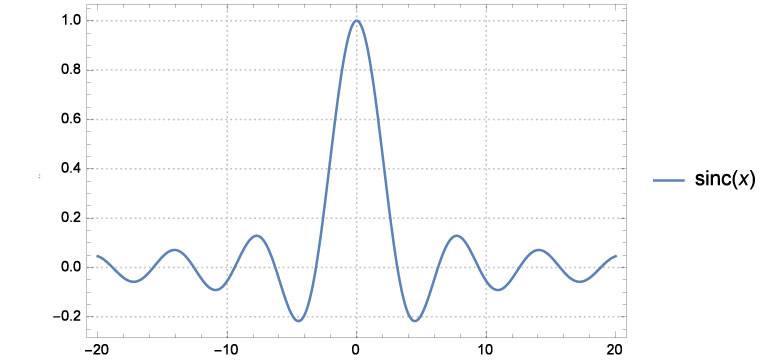
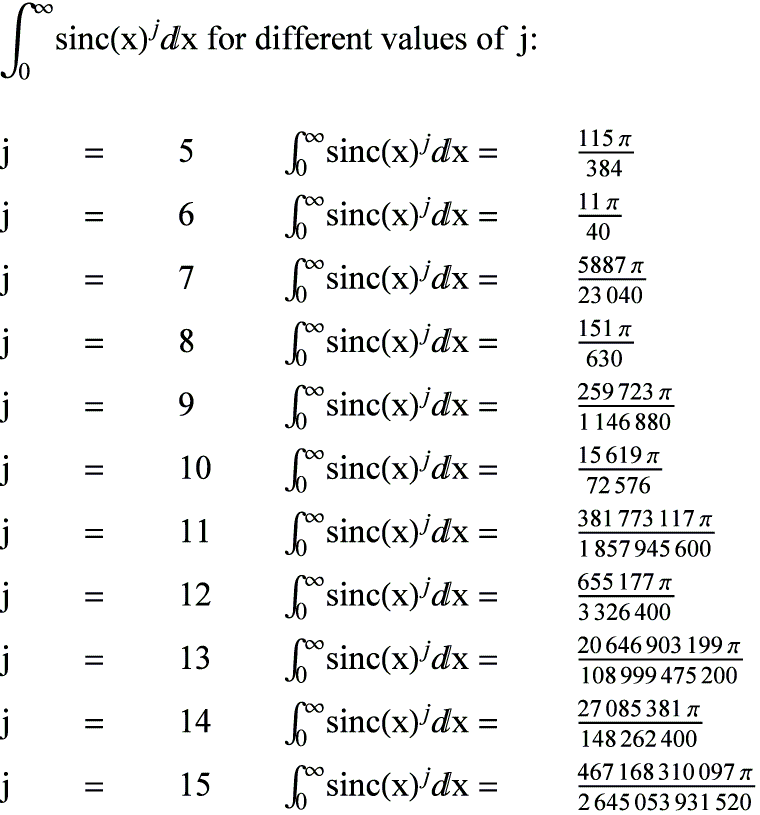
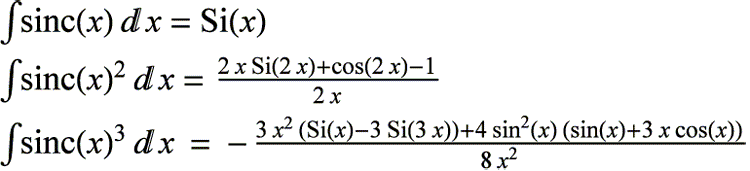The (infamous , or famous , take your pick) sinc function is known to be one of two solutions of the differential equation:
This is a linear second order ordinary differential equation with dependent variable x and independent variable y.
I have tried to explore and find the solutions to this differential equation using mostly computer math software and programs.
The Texas Instruments 92 Plus scientific calculator and the Maple computer algebra system agree and give the same solution :
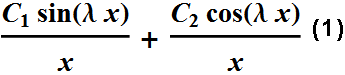 Mathematica gives the following solution:
Mathematica gives the following solution:
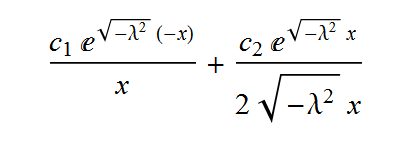 After converting the exponentials to trigonometric functions the expression above and the solution of the differential equation given by Mathematica becomes:
After converting the exponentials to trigonometric functions the expression above and the solution of the differential equation given by Mathematica becomes:
This solution is less simple than (1). Note that if we make the assumption in Mathematica that λ > 0 ,we get the solution:
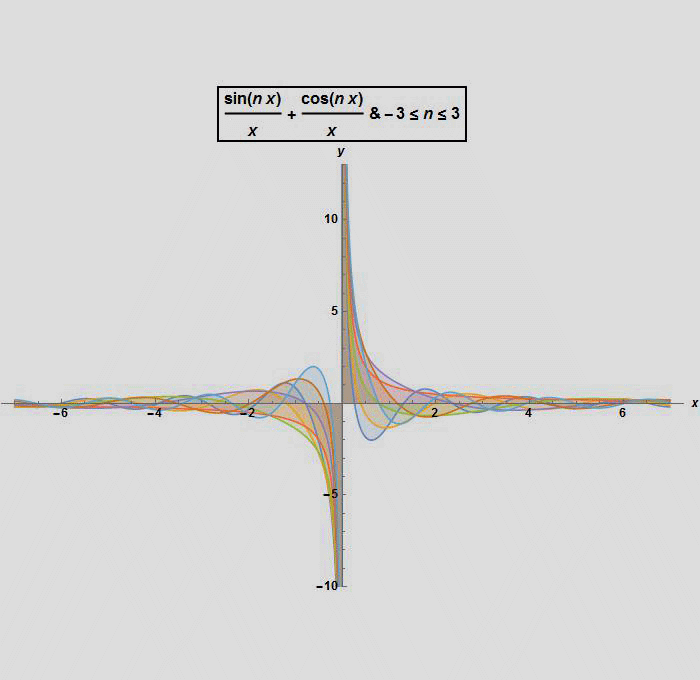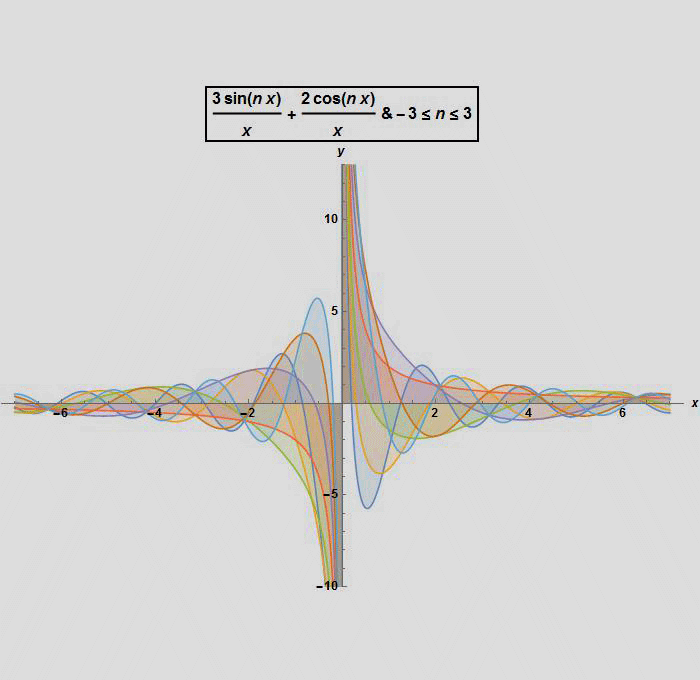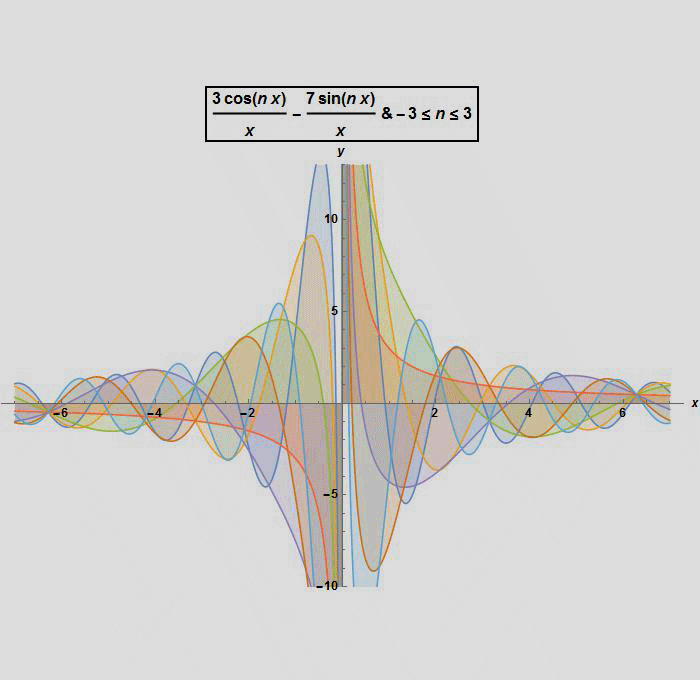
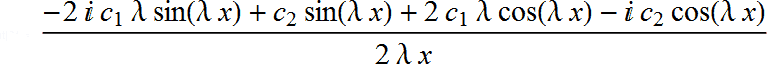 If we try to find the graphical representation of solution (1) for different values of the arbitrary constants c1 and c2 and with λ (or n ) between -3 and 3 ,we get the following graphs:
If we try to find the graphical representation of solution (1) for different values of the arbitrary constants c1 and c2 and with λ (or n ) between -3 and 3 ,we get the following graphs:
Then I tried to take the absolute value of λ in the numerator of (2) for different values of the arbitrary constants , and compared their graphs with the graphs of solution (1) for the same values of the constants. λ in (2) and n in (1) are between 1 and 4.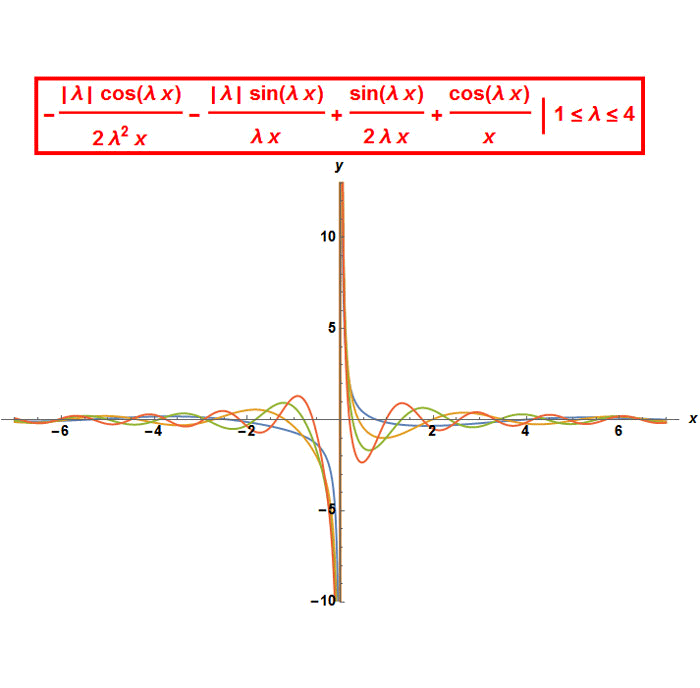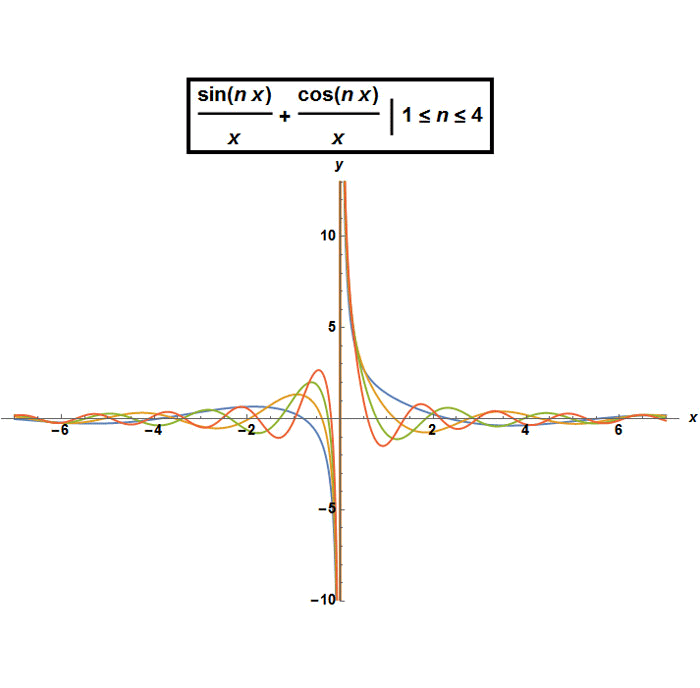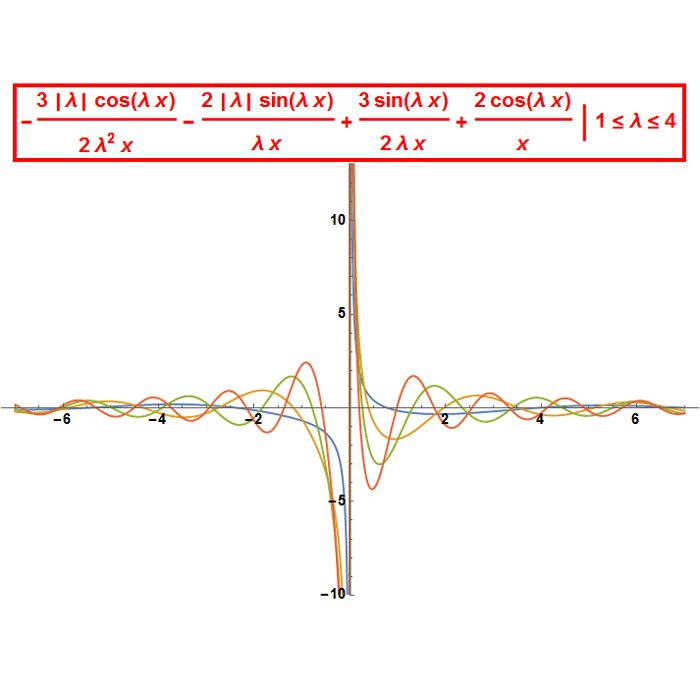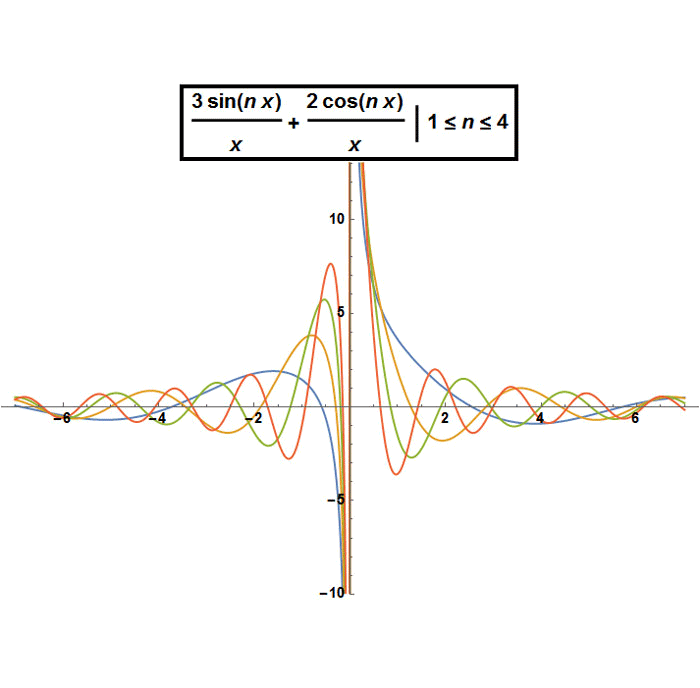
The graphical results are similar but not exactly the same.
Using the Manipulate built-in function in Mathematica , here is an animation of the graphs for solution (1) obtained by varying λ , c1 and c2:
Finally , I will give the solution of a generalized form of the differential equation above
obtained with Mathematica :
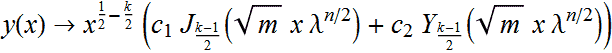 In the solution above , Jμ(x) is the Bessel function of the first kind , and Yμ(x) is the Bessel function of the second kind.
In the solution above , Jμ(x) is the Bessel function of the first kind , and Yμ(x) is the Bessel function of the second kind.

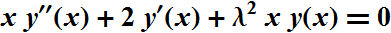

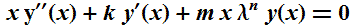
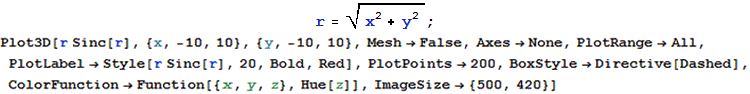
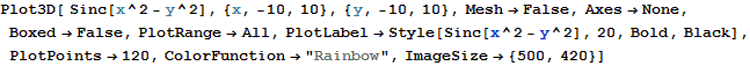
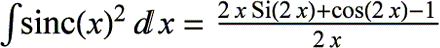
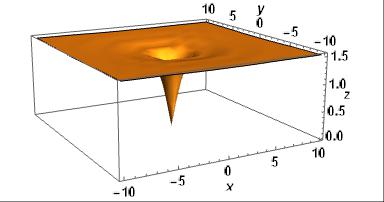
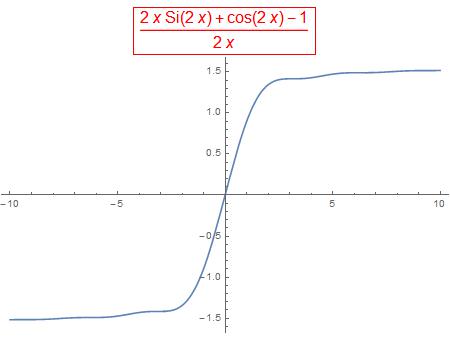 We’ll consider more than one way to graph this function in 3D.
We’ll consider more than one way to graph this function in 3D.

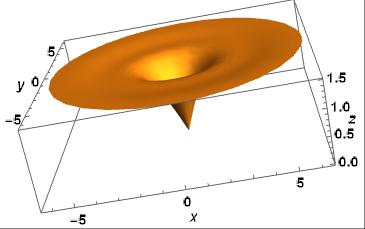
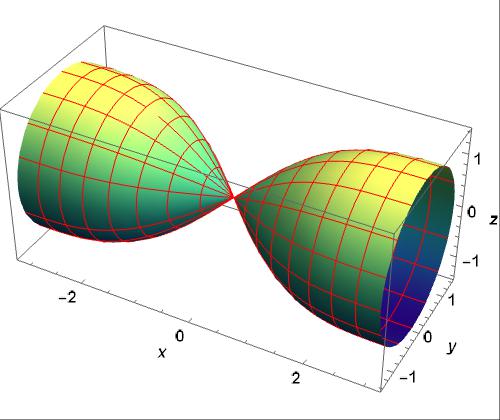

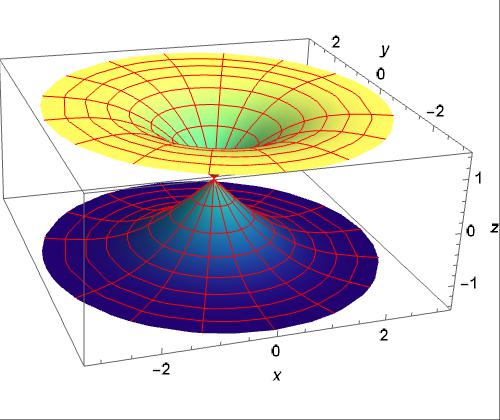

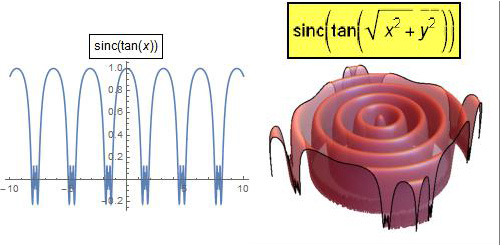
 Mathematica code for the graphs above( rd will be used in the 3D graphs later):
Mathematica code for the graphs above( rd will be used in the 3D graphs later):